この世のあらゆる事象は、数学的に表現できる。
それが僕の揺ぎ無い信念だ。

朝起きて鏡を見ると、てっぺんの髪の毛がピンと明後日の方向を向いていた。
僕の顔の真正面をxy平面、頭頂部を座標(0,0,0)だとすると、(3,2,-5)の方向だ。

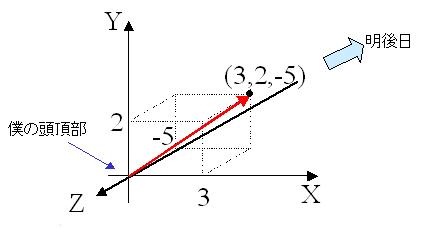
つまり、長さは√(3^2+2^2+(-5)^2) ≒ 7 cm くらいかな。
「男のワックス」をつけて、髪の毛を頭の曲率にぴったりあわせれば、いつもの完璧な僕の出来上がりだ。

慣れた学校への道を最短距離で歩く。
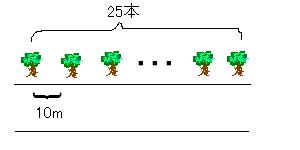
家の前は桜の並木道で、道の端から端まで、10m間隔で綺麗に植えられている。
全部で25本だから、道の長さは25×10・・・いや、危ない危ない。
道の長さを知りたいなら、必要なのは桜の木の本数ではなくて、桜と桜の間のスペースの数だ！だから、道の長さは、(25-1)×10 = 240mだ。

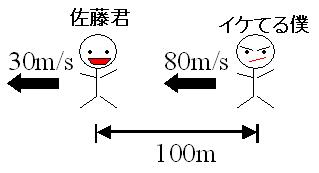
途中、100m先に佐藤君の後姿を発見。
歩くのが遅い佐藤君は、分速30mでのろのろと学校へ向かっている。
トムクルーズの完璧な相似形∽（相似比0.62）のスタイルを持つ僕は、勿論佐藤君より歩くのが早くて、分速80mで歩くことが出来る。つまり・・・
100÷(80-30)=2
ちょうど今から2分後、ここから160m歩いたところで、僕は佐藤君を追い越す筈だ。


「おはよう、佐藤君」
ホラね。

計算通りに進んだことに満足して、学校に辿り着く。
僕のクラスは4年2組。
男の子は21名、女の子は19名。
母集団が19人と、ちょっと少ないが、4年2組の女の子を統計的に見て、可愛い子は概ね金持ちであるという相関関係がある。相関係数は0.6。

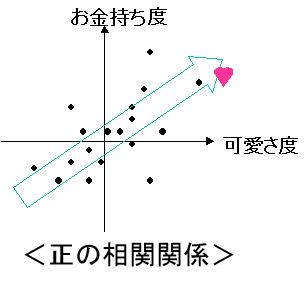
通路を挟んで隣の席の花子ちゃんも、お金持ちで、それに、その、なんていうか、悪くない。
ぼぉっと花子ちゃんの横顔を眺めていたら、不意にこちらを見てにこりと笑った。
心拍数が、y = 2.65x + 85 の一次関数に従って急上昇する。
「今日学校終わったら、うちに遊びに来ない？」
ワォ、なんてこった。
僕の頭の中で、クラッカーが鳴って、色とりどりのテープが
y=-0.625*(x^2)+0.4
の放物線を描いた。

待ちに待ったチャイムが鳴って、僕は一目散に家に駆け戻った。
160m/分の速度で走ったのに、240mの桜並木を駆け抜けるのに、90秒では足りなかったのは、スタミナ不足で40m走るごとに5秒の休憩を必要としたからだ。
実際に何秒掛かったのか計算してみよう。
40m走るのにかかる時間は 40 / 160 = 0.25分 = 15秒
その後5秒の休憩が必要だから、40m走るのには15+5=20秒かかる計算だ。
つまり、240mの桜並木だと、
240 ÷ 40 * 20 = 120秒

・・・だと思うのは数学初心者だ。
最後の40mを走り抜けるのに、走った後の休息の時間は不要である。
だから、実際にかかった時間は、120 - 5 = 115秒だ。

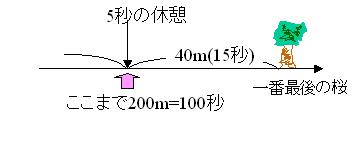
もし時計の秒針を見ていたなら、桜並木を走り抜けた時、走り始める位置と比較して、
115 ÷ 60 = 1 ... 55 = 2 ... -5
-5秒分のずれ、角度にすると、-5 ÷ 60 * 360 = -30度 の位置に来ていたことが 見て取れたことだろう。



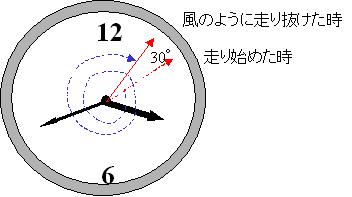
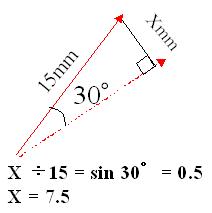
ちなみに、この「走り終えた時の秒針の先の位置A」と「走り始めた時の秒針B」との距離は、点Aから直線Bに垂線を下ろした時の、その垂線の長さだから・・・えーと、その間が30度ということは・・・うーんと、秒針の長さが15mmだから、 ・・・
15 * sin 30 = 7.5mm か。

ちょっと難しかったな。
しかも、答えが出せたところで、全然嬉しくないし。

と、いうか、そんな計算している場合じゃなかった。
僕は花子ちゃんの家に招待されているんだ！
早く支度をして、行かなくちゃ！！

そんなこんなで手早く「男のワックス」と「男の制汗スプレー」で身だしなみを整えた後、僕は、花子ちゃんの家に向かって出発したのであった。


鼻歌を歌いながらスキップで向かう、楽しい道。
が、ここでも僕の行く手を阻む試練が待っていたのである。
魔の住宅街。ここの道はなかなか難しい。
僕の家から辿り着くT字路と花子ちゃんの家へ向かう十字路の角は道の反対側にあるから、 最短距離を行くには、道を対角に進めば良い。
正確には、道の幅が、10m、T字路から十字路までの長さが80mだから、
√(10*10 + 80*80) ≒ 80.6m
80.6m歩けば良い。

・・・筈なのだが、この道には、僕の最大の敵、小池さんちの犬、コタローがいるのだ。

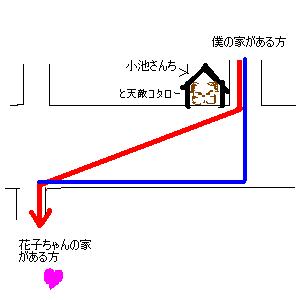
だから、僕はいつも、対角線（赤線）じゃなく、とりあえずコタローから離れるルート（青線）でこの道を進む。その距離90m。9.4mものロスだ！

でも、今日は花子ちゃんの家に1秒でも早く辿り着きたい！
こういう時は、確率計算が有効だ。
今日のような晴れの日のこの時間は、コタローが散歩中でいない可能性は60%。
気分が良い時は吠えてこないけど、コタローの気分が良いのは僕の経験から言うと、25%程度しかない。
つまり、僕が今日、これからコタローに吼えられる可能性は、

(1-0.6)×(1-0.25)=0.3

30%だ。うん、きっと大丈夫。コタローは、吠え掛かってこない。
今日は勇気を出して、対角線で進もう。
そう決意して、ドキドキしながら小池さんちの前を通ったら、待ち構えてたみたいにコタローが吠え掛かってきた。
僕は思わず叫んで加速度1/2 t[m^2/s]で走り出してしまった。
こんな時、僕は確率というものは飽くまで確率でしかないことを改めて実感する。

その5秒後。
加速度をa、時間をtとした時の速度vは、
a = dv / dt つまり、 v = ∫a dt
だから、
v = ∫1/2 t dt = 1/4 t^2 ≒ 6 [ m / s ]
つまり、速度約6m/sに達したところで息が切れて、立ち止まった時、僕はふと気付いた。
おっといけない。紳士たるものシャレたプレゼントの１つでも買っていかないわけにはいかない。
僕は走って通り過ぎてしまった道を少しだけ戻って、花屋に向かった。

よし、薔薇とカーネーションを買おう。
ズボンの後ろポケットを探ったら、千円札が1枚出てきた。
お釣りがなるべく少なくなるように一本以上ずつ下さい、と言って 千円札を渡したら、店員のお姉さんは、花束とお釣り10円をくれた。
実は僕は、どちらが薔薇でどちらがカーネーションか分からないほど花には疎い。
でも大丈夫。
ちょうどこの間、鶴亀算を習ったばっかりなんだ。
今手の中には10円のお釣り。つまりかかった値段は990円。
花は全部で9本ある。
確か薔薇は250円で、カーネーションは70円だった。
これだけ覚えておけば大丈夫。

薔薇がX本で、カーネーションをY本とすると、
250 * X + 70 * Y = 990
X + Y = 9
計算すると、X=2, Y = 7

つまり、2本あるほうが薔薇で、7本ある方がカーネーションってことだ。
計算は完璧だけれど・・・ちょっと微妙な色合いだ。



花子ちゃんちに着くと、花子ちゃんと花子ちゃんのお母さんが待っていてくれた。
「あ、これ、どうぞ」
本当は花子ちゃんに花束を手渡したかったけれど、こういう時はおばさんに渡した方が 後々良い事がある確率が高いのだ。
僕の目論見どおり、あらまぁ、と言って喜んだおばさんは、僕に紅茶とケーキ を勧めてくれた。

おばさんが出してきたのは、半径8cm高さ6cmの小さく上品なホールケーキだった。
お金持ちらしくお上品なケーキカットナイフを持ち出してきて、僕は一瞬感心しかけたが、おばさんの切り分け方は最悪だった。あらあらあらあらあらあら、と言いながら、
A：半径7cm、中心角度60度
B：半径8cm、中心角度50度
という何とも微妙なカットをしたのである。

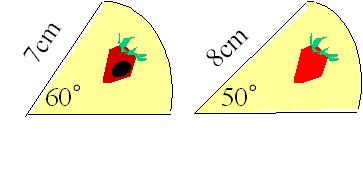
どうぞお好きなほうを、と言われ、僕は反射的に計算をする。

(体積) = π*(半径)*(半径)*((中心角度)/360)*(高さ)

だから、Aの体積は49π[cm^3]。
対してBの体積は53π[cm^3]。

僕は大きいケーキBに手を出そうとしたが、ふと思い直した。
ここのケーキは、まわりのパイ生地部分が美味しいんだ！
ということは、体積ではなく、まわりの部分の表面積を計算するべきなんだ。


(まわりの表面積) = 2π*(半径)*((中心角度)/360)*(高さ)

だから、Aのパイ生地の面積は14π[cm^2]。
対してBのパイ生地の面積は13π[cm^2]。

なんてこった！
僕は、ケーキBに伸ばしかけていた手を慌てて軌道修正して、ケーキAを引き寄せた。

そんな僕の行動がおかしかったのか、花子ちゃんはくすくすと上品に笑った。
か、可愛い・・。
僕の花子ちゃんへの想いは、
[一昨日のLOVE度] + [昨日のLOVE度] = [今日のLOVE度]
フィボナッチ数列のように増大していくばかりだ。→∞

その後、おばさんはウェッジウッドのティカップで、紅茶を勧めてくれた。
先程のケーキとは打って変わって、きっちり150ml、つまり150g弱ずつカップに注いでくれる。
一緒に1辺が0.7cmつまり体積0.343[cm^3]の角砂糖が出されたので、ひとつつまんで入れた。
かき混ぜて一口飲む。
僕の舌は敏感に糖度を測定した。む、この紅茶の砂糖濃度は2.5%だ。
いけない。入れすぎたようだ。
これを僕好みの甘さにするには・・・。
今一口20ml飲んでしまったから今カップに残っているのは約130g。
砂糖濃度が2.5%ということは、今カップ内の砂糖は130×0.025=3.25g。
僕の好みの濃度、2.0%にするには、
3.25 / ( 130 + X ) = 0.02
X = 32.5
あと32.5gの紅茶が必要だ。
花子ちゃんとおばさんは砂糖ナシで飲むらしい。
僕は花子ちゃんのカップを引き寄せ、きっちり32.5gの紅茶を僕のカップに移した。
おばさんのカップの方が近かったのにどうして花子ちゃんのカップに手を伸ばしてしまったのか、自分でも良く分からない。
紅茶は計算通りの糖度になった。だけど何故か、やっぱりちょっぴり甘い気がした。


そんな清く正しいお付き合いが続き、何年かが過ぎたある日、僕は、花子ちゃんに結婚を申し込むことにした。
返事がOKの確率は99.9%。
僕の数学的思考はそんな高確率を導き出しているのに、それでも僕は希望と不安の間を乱数表に従って行ったり来たりの繰りかえし。
だけど、勇気を出して、さあ、プロポーズだ。
結果は・・・。



勿論、花子ちゃんはにっこり微笑んで、「はい」と答えた。



やった！やった！やったー！！OKを貰ったぞ〜！
人生は僕の計算どおり、進みつつある。

こうして僕らは無事婚約を済ませたわけだが、ここで、予定外の出来事が起こったのである。
つまり、結婚式を待たずして僕らの愛の結晶が。




１＋１＝３

人生そんなときもある。